Gil McVean, Philip Awadalla and Paul Fearnhead
Received October 2, 2001.
Accepted January 7, 2002.
Published online March 1, 2002.
GENETICS March 1, 2002 vol. 160 no. 3 1231-1241
https://www.genetics.org/content/160/3/1231
Abstract
유전자 표본의 족보 역사에서 재조합의 양을 결정하는 것은 진화 생물학과 의학 인구 유전학 모두에 중요하다. 그러나 재발 돌연변이는 재조합에 의해 생성된 것과 유사한 유전적 다양성의 패턴을 생성할 수 있으며, 모집단 재조합률의 추정치를 편향시킬 수 있다. 허드슨(2001)은 무한대의 시퀀스 진화 모델에서 인구 재결합률인 4Ner를 추정하기 위해 결합 이론에 근거한 대략적인 우도 방법을 제안했다. 여기서는 재발 돌연변이의 비율이 높은 많은 바이러스나 박테리아와 같은 게놈의 재조합 비율을 추정하는 것으로 그 방법을 확장한다. 또한 다른 순열 기반 방법보다 강력하고 시퀀스 진화의 모델을 잘못 지정할 수 있는 강력한 순열 기반 재조합 탐지 방법을 개발한다. 우리는 이 방법을 바이러스, 박테리아, 인간 미토콘드리아 DNA의 데이터 시퀀스에 적용한다. HIV1과 HIV2 시퀀스 모두에서 검출된 극도로 높은 수준의 재결합은 바이러스 집단 유전자 데이터의 분석에서 재조합을 무시할 수 없음을 보여준다.
Introduction
RECOMBINATION은 게놈의 서로 다른 영역들 사이의 족보 역사의 상관관계를 분해하고 염색체들 사이의 유전적 다양성을 섞는다. 진화생물학에서 재조합의 중요성은 여러 유익한 돌연변이(Fisher 1932; Muller 1932)의 확산을 허용하고 해로운 돌연변이의 축적을 방지하는 새로운 유전자 조합의 생성이다(Muller 1964). 의학 유전학에서는 유전적 표류를 통해 축적되고 재조합에 의해 분해되는 질병 표현형과 유전자 표지의 연관성이 질병과 관련된 돌연변이의 지도화(Pritchard and Przeworski 2001)의 핵심이다.
재조합의 발생은 진화적 추론에도 실질적인 영향을 미친다. 인구유전학자들의 경우, 재조합은 게놈에 대한 계보학적 이력을 평균하여 진화적 확률성의 영향을 감소시킨다. 이와는 대조적으로, 종양성 추론의 전통적인 방법들은 일반적으로 재조합의 부재를 가정한다. 만약 그 가정이 틀리면, 유전자 서열의 진화 이력에 대한 추론은 오해의 소지가 있을 수 있다(Schierup과 Hain 2000). 따라서 재조합은 종내 변동의 분석에 중요한 문제가 된다.
유전자 염기서열에서 재조합이 발생하는 비율을 추정하지 않고 이를 검출하기 위한 다양한 비모수적 방법이 개발되었다. 어떤 사람들은 유전자의 다른 부위가 서로 다른 이력을 가지고 있는지를 질문하기 위해 계통발생적 방법을 사용한다(Grassly and Holmes 1997; McGuireet al. 2000년)은 희귀 재조합 유전자형을 식별하는 것을 목표로 한다. 다른 방법들은 대부분의 eukaryote 종의 유전자들 사이에서 일어나는 것과 같이 재발하는 재조합의 존재를 유추하는 것을 목적으로 한다. 이러한 방법 중에서 물리적 거리와 조치의 관계 등 재조합에 민감한 요약통계량이나 연계불균형 지표(Lewontin 1964; Maynard Smith 1999)를 고려하는 사람도 있다. 다른 방법에서는 재조합이 없다는 가정 하에 추론된 계통생성 나무의 특성을 고려한다(Maynard Smith and Smith 1998; Worobey 2001). 방법은 서로 다른 조건에서 재조합을 통계적으로 탐지하는 능력과 시퀀스 진화의 기본 모델의 정확한 특성화에 대한 민감도가 다양하다(Maynard Smith 1999; Meunier 및 Eyre-Walker 2001).
그러한 방법으로는 재조합이 발생하는 비율을 추정할 수 없다는 것은 심각한 한계다. 재조합 비율을 특징짓는 것은 연관 연구의 힘을 분석하고, 계통생성 방법의 신뢰성을 평가하고, 약물 내성을 부여한 것과 같은 유리한 돌연변이가 유전적 배경 사이에 퍼질 수 있는 비율을 예측하는 데 중요하다. 동종검사(Maynard Smith and Smith 1998)와 파생상품(Worobey 2001)과 같이 재조합을 검출하기 위한 일부 비모수적 방법은 데이터가 자유재조합과 완전한 부조화의 극단으로부터 얼마나 멀리 떨어져 있는지를 특성화한다. 그러나 그러한 특성과 어떤 근본적인 진화 모델의 매개변수 사이에는 직접적인 관계가 없다. 그 결과, 유전자나 종과의 비교는 문제가 되고 있으며, 데이터 세트의 재조합 수준이 다른지 통계적으로 검사할 수 있는 방법이 거의 또는 전혀 없다. 재조합 비율의 모델 기반 추정은 거의 확실히 현실의 단순화인 기본 모델에 의존한다. 그러나 얻은 이점은 서로 다른 데이터 집합 간의 비교 용이성, 관심 문제에 대한 예측 능력, 진화의 모델이 기반 프로세스의 적절한 특성화인지 여부를 테스트할 수 있는 가능성이다. 또한 파라메트릭 모델을 사용하여 재조합이 있는 모델과 없는 모델에서 데이터의 가능성을 비교함으로써 재조합의 존재를 시험할 수 있다(Brownet al. 2001).
유전자 서열에 대한 재조합의 영향을 설명하는 데 적합한 진화 모델은 무엇인가? 결합 이론은 비과대적 세대, 일정한 모집단 크기, 선택이나 이주가 없는 대규모 피셔-라이트 인구로부터 샘플링된 결과의 족보적 이력에 대한 통계적 설명을 제공한다(Kingman 1982; Hudson 1991). 이 프레임워크 내에서, 표본 기록에 대한 재조합의 영향은 절대 재조합 비율이 아니라, 교차하는 세대당 유전자당 유전자당 생성물인 Ne(유전 지도 길이), r, 유효 모집단 크기인 Ne(Griffiths and Marjoram 1996b)의 함수다. 이러한 변수들 중 하나에 대한 사전 정보가 없다면, 이러한 변수들의 산물만 추정할 수 있는데, 흔히 ρ = 4Ner(동일하게, 재조합율과 돌연변이율, r/μ, 모집단 돌연변이율 θ = 4Neμ)로 표기된다. 합성은 시간 분산 모집단 크기, 이주 및 일부 선택 형태를 포함하도록 쉽게 확장할 수 있다(Hudson and Kaplan 1994; Bravermanet al. 1995). 이러한 더 복잡한 상황에서 유전자 표본에 대한 재조합의 영향도 다른 매개변수에 따라 달라진다. 그러나 일반적으로 모집단의 현재 유효인구 규모와 절대 재조합률의 산물은 유전적 다양성의 패턴에 대한 재조합의 영향을 결정하는 핵심 결정 요인이다.
결합의 틀 안에서, 인구 재결합률의 추정자로 몇 가지 방법이 제안되었다. 허드슨(1987)은 쌍별 차이의 분산을 기초로 모멘트 추정기를 도출했다. Hey와 Wakeley(1997)는 모든 사이트 쌍과 네 개의 시퀀스 집합에 대해 분석적으로 파생된 가능성을 결합한 방법을 개발했다. 월(2000년)은 happlotype의 수를 관측할 가능성을 최대화하는 4Ner의 값을 찾고 유추된 최소 재조합 사건 수를 찾자고 제안했다(Hudson과 Kaplan 1985년). 인구 재결합률에 대한 전체 우도 추정기(Consumentation rate)도 조합에 기초하여 개발되었다. 이들은 계산적으로 집약적인 몬테카를로 방법을 사용한다. 그리피스와 마르조람(1996a)은 중요도 샘플링에 기초하여 방법을 설명한 반면 쿠너 외 연구진은 중요한 샘플링에 기초하여 방법을 설명했다. (2000) Metro-Hastings 거부 몬테카를로 마르코프 체인(MMC) 방법을 개발하였다. 최근 Fearnhead와 Donnelly(2001)는 중요도 샘플링 방법을 상당히 개선했다. 그렇더라도 전체 우도 방법은 계산적으로 집약적이며 많은 데이터 집합에서 실질적으로 불가능하다.

최근 허드슨(2001)은 모든 쌍별 비교의 결합 가능성을 결합하여 인구 재결합률을 추정하기 위한 특별 방법을 제안했다. 4Ner의 추정은 빠르고, 이 방법은 허드슨의 초기 모멘트 추정기(Hudson 1987) 및 기타 임시 접근법(Hudson 2001)에 비해 편향과 분산 측면에서 잘 수행된다. 이 방법은 시퀀스 데이터에서 사용 가능한 모든 정보를 사용하고 다중 비교의 조합에서 비독립성을 도입하지는 않지만 유연하고 잠재적으로 표준 결합으로부터의 편차를 통합하도록 확장할 수 있다. 허드슨(2001)의 4Ner 추정치는 복합 우도 추정치(CLE)로 불린다.
이 글에서는 재조합 분석에 매우 중요한 문제를 고려한다: 많은 바이러스나 박테리아와 같은 게놈에서 재조합의 검출과 추정으로, 일부 사이트는 표본의 역사에서 여러 변이를 경험했을 정도로 치환율이 높다. 이 문제는 재발 돌연변이가 재조합의 효과와 유사한 유전적 변동성의 패턴을 생성할 수 있기 때문에 중요하다(그림 1) 특히, 한 쌍의 분리 부위에 대한 4개의 아플라타입 모두 존재하기 때문이다. 무한대 모형에 따르면, 그러한 비호환성은 재조합을 위한 증거로 해석될 수 있으며, 따라서 재결합률의 추정치는 상향으로 치우치게 될 것이다. 마찬가지로 재결합 유무를 위한 우도 비율 시험은 돌연변이 모델의 잘못 지정, 특히 비율 이질성에 의해 야기될 수 있는 분리 현장의 돌연변이 비율의 과소평가에도 민감할 것이다.
이러한 문제를 해결하기 위해 우리는 유한한 돌연변이 모델을 허용하도록 허드슨의 복합 우도법(Hudson 2001)을 확장했다. 또한 재조합이 없다는 가설(4Ner = 0)을 검정하기 위해 순열 기반 검정(우도 순열 검정)을 제안한다. 비독립성으로 인해 복합 우도 표면의 해석이 문제가 되므로 복합 우도로부터 신뢰 구간을 추정하기보다는 순열 기반 접근법을 사용한다. 분석된 대부분의 사이트가 다중 변동을 경험했더라도 복합 우도 추정기가 잘 작동하고, 우도 순열 테스트가 재조합을 검출하기 위한 이전의 순열 기반 방법보다 더 강력하다는 것을 알게 되었다. 또한 우리는 4Ner의 재조합 및 추정에 대한 시험 모두에 대한 시퀀스 진화 모델의 오정화의 영향을 고려한다. 우리는 우도 순열 테스트가 동종 시험(Maynard Smith and Smith 1998)이나 정보 사이트 테스트(Worobey 2001)와 달리 오정화에 강하며, 4Ner의 추정도 시퀀스 진화 모델의 사소한 오정화에 강하다는 것을 보여준다. 우리는 바이러스, 박테리아, 인간 미토콘드리아의 여러 경험적 데이터 집합에 우도 순열 시험과 추정 절차를 적용한다.
Method
4Ner의 복합 우도 추정: 첫째, 표준 Fisher-Right 인구 모델에 따라 모집단 재결합률을 추정하기 위한 허드슨(2001)의 접근방식의 구현을 개략적으로 설명한다. 허드슨(2001)의 방법과 여기에 제시된 방법 사이의 중심적인 차이는 샘플의 역사 동안 현장에서 다중 돌연변이가 발생할 수 있는 시퀀스 진화의 모델을 허용한다는 것이다. 시퀀스 진화의 임의 모델을 사용할 수는 있지만, 우리는 일련의 모든 현장이 가역성 대칭 돌연변이를 가진 2알레 모델에 부합한다는 단순화 가정을 한다. 즉, 사이트당 돌연변이의 비율은 μ이며 사이트 전체에서 일정하다. 따라서, 우리는 둘 이상의 분리항목이 없는 사이트로 분석을 제한한다. 시퀀스 진화의 더 복잡한 모델에 대한 방법의 확장은 향후 연구에 맡겨진다. 그러나, 시퀀스 진화의 실제 모델이 가정된 모델보다 상당히 복잡하더라도, 그 방법이 잘 수행되는 것으로 보인다는 점에 주목할 필요가 있다(아래 참조).
추정 절차는 네 단계로 구성되어 있다. 초기 단계는 Watterson 추정치의 대략적인 유한 사이트 버전에서 사이트당 모집단 돌연변이 비율(θ = 4Neμ)을 추정하는 것이다.

여기서 S는 분리 현장의 수, L은 분석된 시퀀스의 총 길이, n은 샘플링된 유전자 시퀀스의 수입니다. 두 번째 단계는 데이터 내 모든 분리 사이트 쌍(알레이가 두 개 이상인 사이트 제외)을 고려하여 동등한 세트로 분류하는 것이다. 예를 들어 가정된 돌연변이 모델에서 한 쌍이 순서 데이터 {AA, AT, TA, TA, TA, AA}을(를) 가지고 있고 다른 한 쌍이 다른 {G, CC, CG, GG, GG, 01}을(를) 가지고 있다면 이는 순서가 정렬되지 않은 {00, 00, 10, 10, 0, 0, 0}인 경우 각 현장의 희귀 알레르를 나타낸다. 유형 수(프로그램의 실행 시간을 결정)는 시퀀스 수, 다양성 수준 및 가정된 돌연변이 모델의 복잡성에 따라 달라진다.
세 번째 단계는 Fearnhead와 Donnelly(2001)의 중요도 샘플링 방법을 사용하여 θ의 추정 값, 대칭, 반전성 돌연변이 모델 및 재결합률 범위(일반적으로 0 ≤ 4Ner ≤ 100)에서 설정한 각 등가물의 가능성을 추정하는 것이다. 또한 허드슨(2001)에서 구현한 것과 유사한 간단한 몬테카를로 추정 방법을 사용하여 중요도 표본 추출 방법에 의해 추정된 우도의 정확성을 검사했다(결과가 표시되지 않음).
최종 단계에서 전체 시퀀스(4Ner)에 대한 모집단 재결합률의 추정치는 모든 쌍별 비교의 가능성을 결합하여 구한다. 복합 우도는 다음과 같이 주어진다.

여기서 ℓ(Xij|4Nerij)은 주어진 사이트 i와 j를 분리하기 위한 데이터의 로그 가능성이다.
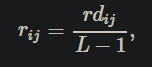
나 그냥 j와 순서(즉, 우리는 재조합의 유전자에 일정한 속도 추정)L은 총 길이 사이트를 분리시키는 것(뉴클레오타이드의)어디 dij이 물리적 거리이다. 4Ner의 판단은 가장 복합 로그 가능성이 지닌 가치로 간주된다.
바이러스와 박테리아와 같은 게놈,의 경우 재결합에 대한 gene-conversion 모델 더 교차 모델, 물리적 거리 사이의 관계보다 적절하다.재결합률로 모델링 하였다.

여기서 c는 유전자 변환의 시작에 대한 기준 비율 당이고 t는 평균 유전자 변환 트랙 길이(지수 분포 추정, Friseet al. 2001)이다. 이러한 유형의 모델은 미토콘드리아와 같은 원형 게놈에도 적용될 수 있는데, 여기서 dij는 원의 두 점 사이의 최소 거리(Wiuf 2001)이다. 유전자 변환 속도와 평균 트랙 길이 모두를 공동 추정하는 것은 가능하지만, 실제로 우리는 평균 트랙 길이를 고정하고 복합 파라미터를 추정한다.

이것은 유전자 변환에 의해 야기된 멀리 연결된 두 위치 사이의 재조합의 인구 비율이라고 생각할 수 있다.

단순 데이터 세트와 4Ner의 낮은 값의 경우 Fearnhead 및 Donnelly(2001)의 방법으로 추정된 전체 우도 표면과 복합 우도 표면을 비교할 수 있다. 그림 2는 단일 사례에 대한 두 표면의 비교와 최대우도 추정기(MLE)의 공동 분포와 100개의 시뮬레이션 데이터 세트에 대한 4Ner의 CLE 점 추정치(n = 50, θ = 4Nner = 3)를 보여준다. 단일 예제(그림 2A)의 경우, 복합 우도 곡선은 ML 추정치와 매우 유사한 점 추정치를 가지지만 다중 비교에 의해 도입된 비독립성 때문에 더 높은 곡선이다. 4Ner의 두 추정치(완전 우도/합성 우도)에 대한 통계량은 중위수, 2.4/3.8, 분산, 9.1/15.6, 실제 값에서 2인자 내의 비율(0.50/0.52)이다. 복합 우도 추정치와 최대 우도 추정치 사이의 상관관계는 0.78이다(그림 2B).
허드슨(2001)은 데이터가 무한대 모형에 부합하는 경우에 대한 복합 우도 추정기를 특징으로 했다. 치우침과 분산 측면에서, 추정기는 상당한 분산을 가지고 있지만, CLE는 모집단 재결합률을 추정하기 위한 더 나은 임시 방법 중 하나이다. 그러나 이는 MLE(그림 2)에도 해당되며, 대체로 계보 과정에 내재된 확률성의 반영이다. 그러나 전우도는 서로 다른 값의 상대적 우도에 대한 추정치를 제공하지만, 복합 우도 곡선의 해석 가능한 의미는 쉽게 없다. 4Ner 추정치에 대한 신뢰 구간은 광범위한 시뮬레이션을 통해서만 얻을 수 있다(Hudson 2001).
우도 순열 검정: 우리는 재조합의 존재에 대한 간단한 테스트를 제안한다. 재조합이 없는 모델에서 균일한 돌연변이 비율을 가정하면 사이트는 교환이 가능하다(자유 재조합이 있는 경우에도 마찬가지다). 즉, 데이터를 관측할 가능성은 현장이 발생하는 순서와 무관하다. 어떤 재조합이 있으면, 사이트들은 더 이상 교환할 수 없다. 왜냐하면 밀접하게 연결된 사이트들은 서로 상관관계가 있기 때문이다. 따라서 데이터를 관측할 가능성은 현장의 순서에 따라 달라진다. 재조합을 위한 우도 순열 시험은 이 특성에 기초한다; 우리는 데이터 집합에 대한 최대 복합우도(프로세스에서 4Ner를 추정)를 찾은 다음 위치별로 사이트를 구분하고 각 순열에서 최대 복합우도(및 해당 값 4Ner)를 찾는다. 복합우도가 원래 데이터와 같거나 큰 순열 데이터 세트의 비율이 계산된다. 이 비율이 선택된 유의 수준보다 낮으면 재조합을 위한 증거가 있다고 결론짓는다.
분리현장의 순열을 기초로 재조합을 검출하는 방법에는 몇 가지가 있다. 거리와의 연계불균형(r2 또는 |D′|) 요약통계량의 붕괴를 감지하기 위한 재조합에 대한 순열시험은 인간 미토콘드리아(Awadalaet al)에 재조합의 존재를 시사하는 데 사용되었다. 2000년) 및 플라스모듐 팔시파룸(Conwayet al. 1999년)과 드로소필라 멜라노가스터 게놈의 재결합률이 낮은 지역(Miyashita와 Langley 1988년)이다. 또 다른 순열 테스트(G4)는 Meunier와 Eyre-Walker(2001)에 의해 제안되었으며, 이 테스트는 가능한 4가지 선형을 모두 가진 사이트 쌍 사이의 거리의 합을 순열 데이터 세트의 분포와 비교한다. 우리는 우도 순열 시험의 검정력을 다른 순열 기반 시험과 비교했다.
Models of sequence evolution: 일부 또는 모든 현장에서 높은 돌연변이율을 경험하는 게놈을 반영하는 일련의 시퀀스 진화 모델에 따라 복합 우도 추정기와 우도 순열화 시험 모두를 특성화한다. 우리는 가능한 상황의 다양성을 나타내기 위해 4개의 캐리커처 모델을 선택했다. 무한 사이트: 모든 부위는 동일한 낮은 돌연변이 비율(반복 = 0.01)을 가지며 우도 추정 단계에서 사용되는 2알레 대칭의 역전형 돌연변이 모델을 준수한다. 이는 인간의 핵 로키에 대해 가정할 수 있는 최선의 경우 시나리오(효과적으로 무한 확장 사이트)를 나타낸다(고주파 CpG 디뉴클레오티드 제외). 하이퍼마블: 대부분의 사이트(99.5%)는 무한사이트 모델(단위 = 0.005)에 효과적으로 부합하지만, 일부(0.5%)는 100배 높은 돌연변이율을 가진다. 모든 부위는 대칭적이고 되돌릴 수 있는 돌연변이 모델을 따른다. 이는 포유류의 분석 또는 미토콘드리아 게놈에 고화성 CpG 디뉴클레오티드(hypermable CpG dinucleotide)가 포함될 때 나타나는 것과 같이 극단적인 비율 변동을 반영하기 위해 선택된다. 복잡함: 이는 강한 기저 구성 변동과 돌연변이 비율 변이가 특징이다. 구체적으로는 HKY(Hasegawa, Kishino, Yano) 돌연변이 모델(Hasegawaet al. 1985)이며, 기본 주파수는 0.4, πC = 0.1, πA = 0.4, πG = 0.1, 전환-전환율 2, 기저값 변이율의 지수 분포가 있다.
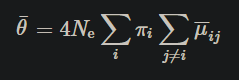
μ'ij는 base i에서 base j까지의 세대별 평균 돌연변이 비율이다(지수 분포에서). 이 모델은 염기 조성 편향이 강한 프로카리오테 게놈의 시퀀스 진화의 복잡성을 반영하기 위해 선택되었다. 유한 사이트: 모든 부위는 동일한 높은 돌연변이 비율(반복 = 0.5)을 가지며 2알레 대칭, 반전성 돌연변이 모델을 준수한다. 이 경우 각 분리 사이트는 표본 이력에서 평균 2.6개의 돌연변이를 경험한다. 이 모델은 인간 면역결핍 바이러스(HIV)와 같은 역발생의 동의어 사이트에서 일어나는 극단적인 수준의 다형성을 나타낸다. 데이터는 null 4Ner = 0 및 4Ner = 10에 따라 시뮬레이션되며, n = 50에 대해, 그리고 선택한 시퀀스 길이로 평균 분리 사이트 수가 40–50 범위에 있다. 이상적으로는 각 시뮬레이션 데이터 세트에 대해 데이터에서 추정된 θ 값에 대한 가능성을 계산해야 한다. 그러나 추정기 속성의 정확한 특성화를 제공하는 데 필요한 반복실험 횟수가 많은 경우, 각 데이터 집합에 대한 가능성을 계산하는 것은 사실상 불가능하다. 대신 we, 0.01, 0.1, 0.5의 서로 다른 세 가지 값에서 우도를 추정하여 각각에 대한 결과를 시뮬레이션 데이터에서 추정된 θ 값의 평균 및 표준 편차와 함께 제시한다. 이 접근방식의 한 가지 장점은 재조합의 검출과 추정에 대한 모델 오타입의 심각성을 특징 지을 수 있다는 것이다.
Empirical data: 우리는 바이러스, 박테리아, 인간 mtDNA로부터 얻은 일련의 경험적 데이터 집합에 우도 순열 시험과 모집단 재결합률의 추정을 모두 적용했다. 이전 분석(Suerbaumet al. 1998; Awadalaet al. 1999; Worobeyet al. 1999; Ingmanet al. 이러한 데이터 세트 중 2000; Worobey 2001)은 C형 간염 바이러스(HCV)와 mtDNA(Ingmanet al)에서 효과적으로 클론화되기까지 다양한 수준의 재조합을 보였다. 2000; Worobey 2001). 헬리코박터 파일로리에서 자유롭게 재결합한다(Suerbaumet al. 1998). 이러한 데이터 집합 중 어느 것도 피셔-라이트 모집단의 무작위 표본을 나타내지 않지만, 통합 분석 방법에 의해 예상된 것처럼, 그 결과는 보다 적절한 표본의 상황을 나타낼 가능성이 높다.
바이러스 게놈: 데이터 집합은 다음과 같다. HCV, 완전한 게놈 서열 6개(Worobey 2001; 전 세계 샘플), 홍역, 헤마글루틴 유전자의 50개 서열(Woelket al. 2001; 전 세계 샘플), 뎅기 DEN-1 바이러스, 결합 캡시드 C 7세트, 프리엠브레인/membrane prM/M, E 유전자(Worobey al 1999; 전 세계) HIV2 아형 A, 21개의 엔비 유전자(Kuikenet al. 2000; 전 세계) 및 HIV1 하위 유형 B, 93개의 환경 유전자 시퀀스(Kuikenet al. 2000; 전 세계).
박테리아 게놈: H. 필로리 데이터 세트는 플라아 유전자의 33개 시퀀스였다(전 세계적으로, Suerbaumet al. 1998).
미토콘드리아 게놈: 데이터 세트는 아와달라 외 연구진(1999; 전 세계)의 분석에서 45개의 부분 게놈 시퀀스와 잉그만 외 연구진 분석에서 53개의 완전한 게놈 시퀀스였다. (2000).
Result
Estimating 4Ner with recurrent mutation: 지금까지 인구 재조합률 추정기는 일반적으로 각 분리 부지가 단일 돌연변이의 결과라는 무한대 가설 하에서 특성화되었다. 많은 생물학적으로 현실적인 상황에서, 비록 무한대의 모형이 표면적으로 그럴듯하다고 할지라도, 이러한 가정은 정당화될 수 없다. 예를 들어, 500개의 연계된 사이트(n = 50 및 = = 0.009)의 계보에서 20개의 돌연변이가 발생하는 경우, 최소 1개의 사이트가 재발 돌연변이를 경험할 확률은 30% 미만이며, 재결합이나 돌연변이 비율의 사이트 간에 변동이 있을 경우 더 높아질 것이다. 많은 바이러스나 박테리아와 같이 돌연변이 발생률이 높은 유기체에서는 많은 수의 부위가 다중 돌연변이를 경험했을 수 있다.
재발 돌연변이는 재조합의 효과를 닮은 유전적 변동성의 패턴을 만들 수 있기 때문에(그림 1) 시퀀스 진화의 유한한 부분 모델을 설명할 수 있는 재조합률을 추정하는 방법을 개발하는 것이 중요하다. 우리는 허드슨(2001)의 인구 재결합률 추정을 위한 복합우도법, 4Ner를 조합의 프레임워크 내에서 확장하여 현장의 표본 이력에서 다중 돌연변이를 경험할 수 있는 모델을 통합했다. 우리의 접근방식은 가능한 가장 간단한 유한 종족 진화 모델(현장에 걸쳐 대칭 역전 돌연변이와 일정한 돌연변이를 갖는 2알레 시스템)을 사용하고 생물학적 다양성을 반영하기 위해 선택된 시퀀스 진화의 다양한 캐리커처 모델 아래에서 방법이 어떻게 수행되는지 조사하는 것이다.

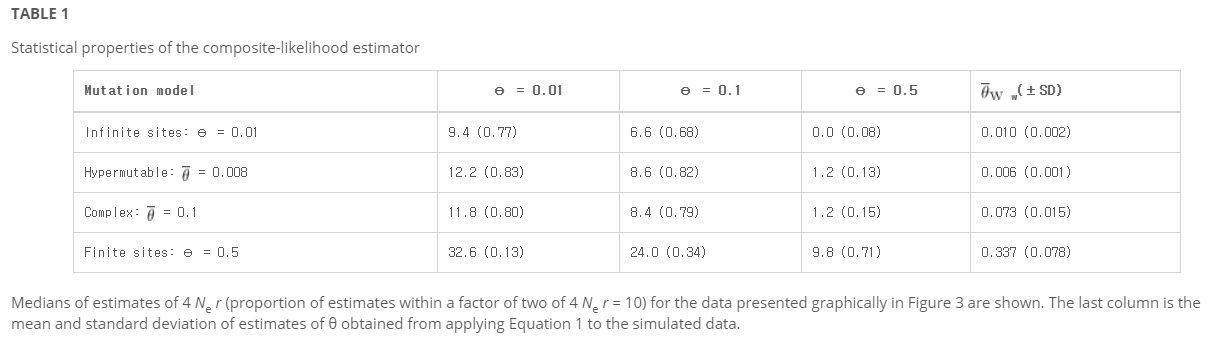
그림 3은 4개의 캐리커처 모델(n = 50 및 4Ner = 10)에서 시뮬레이션한 데이터에 대한 4Ner에 대한 점 추정치 분포와 θ의 세 가지 다른 값인 0.01, 0.1 및 0.5에서 추정된 우도 분포를 보여준다. 표 1에는 실제 값에서 2의 요인 내에 있는 추정치의 중위수와 비율도 방정식 1에서 구한 θ 추정치의 평균과 표준 편차와 함께 제시되어 있다.
예상대로 θ의 참값과 우도 추정에 사용된 값 사이에 상당한 차이가 있을 때, 4Ner의 추정치는 강하게 편향된다. value의 참값이 우도 추정에 사용되는 값보다 낮을 경우, 4Ner의 추정치는 하향 편향된다. 반대로 contrast의 참값이 우도 추정에 사용되는 값보다 클 때, 4Ner의 추정치는 위쪽으로 치우친다. 그러나 θ의 정확한 값으로 우도를 추정할 때 변이율이 낮을 때와 마찬가지로 변이율이 매우 높을 때(그림 3, 오른쪽 아래 대 왼쪽 위) 추정기도 거의 비슷하게 성능을 발휘한다는 것을 알 수 있다(그림 3, 오른쪽 아래 대 왼쪽).
그림 3과 표 1의 가운데 두 행은 어느 정도 생물학적 복잡성을 나타내는 모델에서 시뮬레이션한 데이터에 단순 돌연변이 모델을 적용하는 효과를 보여준다. 하이퍼마블 모델과 복합 모델 모두 사이트 간에 강력한 비율 변동이 있지만, 추정기 속성은 최상의 시나리오 하에서보다 더 나쁘지는 않으며, θ의 추정치는 합리적인 4Ner 추정치를 이끌어내는 범위 내에 있다. 간단히 말해서, 모집단 재결합률의 복합 우도 추정자는 기초 돌연변이 모델의 사소한 오타에 대해 강건하다. 이 결론은 실제 데이터 세트에 대한 CLE의 사용에 대한 정당성을 제공하기 때문에 매우 중요하다.
Detecting Recombination: 위에 제시된 결과는 재발 돌연변이 비율이 높은 게놈에서도 합성우도법에 의해 추정된 4Ner의 값이 의미 있다는 어느 정도 자신감을 줄 수 있다. 그러나 CLE 프레임워크 내에서 다루기 어려운 한 가지 중요한 질문은 4Ner = 0이라는 가설을 거부할 수 있는가 하는 것이다. 재조합을 위한 직접적인 실험 증거는 많은 게놈에 대해 얻기가 어려울 수 있다(특히 유전적 교환이 매우 드문 경우). 따라서 간접적인 모집단 유전자 기반 충족이 중요하다.재조합 탐지용 호드 그리고 그러한 방법들이 시퀀스 진화의 모델의 오타를 통해 잘못된 긍정을 만들어내지 않아야 한다는 것도 마찬가지로 중요하다.
우리는 재조합의 존재에 대한 시험 수단으로 우도 순열 시험을 제안했다. 표 2는 시퀀스 진화의 동일한 4개의 캐리커쳐에 대해 수행된 전력 분석 결과를 보여주고, 다시 again의 세 가지 값에 따른 가능성을 추정한다. 또한 우리는 재조합의 존재에 민감한 데이터의 요약을 고려하는 재조합을 위한 다른 순열 기반 시험과 우도 순열 시험의 힘을 비교한다.
중요한 결과는 우도 순열 테스트가 일관되게 모집단 유전자 데이터에서 재조합을 검출하는 가장 강력한 순열 기반 방법이라는 것이다. 무한대 데이터의 경우 거의 96%의 사례에서 재조합이 검출되며, 다른 테스트의 경우 최대 80%가 검출된다. 우도를 추정하는 데 사용되는 모형이 실제 모형과 매우 다른 경우에도 검정의 검정력은 상당하다. 예를 들어 유한점 모형에 의해 생성된 데이터를 with = 0.5로 하여 θ의 정확한 값을 사용하여 우도를 계산하는 경우의 83%에서 재조합이 검출되는 반면, = = 0.01을 사용하여 우도를 추정하는 경우는 82%이다. 이와는 대조적으로 4개의 게이메트가 모두 존재하는 쌍의 분포에 크게 의존하는 방법(|Dd|, G4)은 이처럼 높은 수준의 돌연변이(각각 51%, 39%) 하에서 전력을 크게 감소시켰다. 우도 순열 시험이 검정력을 감소시킨 한 가지 상황은 value의 참 값이 우도를 추정하는 데 사용된 값보다 훨씬 낮은 경우지만, 경험적 데이터에 대해서는 그러한 상황이 발생하지 않을 것이다. 또한 생물학적으로 그럴듯한 시퀀스 진화의 모델에 대해서는 r2와 물리적 거리 사이의 상관관계를 이용하여 재조합을 검출하는 힘이 |D′| 또는 G4보다 일관되게 크다는 점도 주목할 필요가 있다.
DISCUSSION AND APPLICATION
복합 우도 방법과 우도 순열 시험은 유전적 변동성 패턴에 대한 재조합의 영향을 평가하기 위한 강력한 접근방식을 제시한다. 유전자 염기서열 진화에 영향을 미치는 돌연변이 및 대체 과정이 복잡하고 어떤 단순한 모델에 의해서도 완전히 특성화될 가능성이 없는 경우에도, 간단한 모델의 사용은 재조합을 감지하고 모집단의 재결합률을 추정하는 현저하게 강력한 방법을 제공한다. 새로운 접근법이 실제 데이터에 어떻게 작용하는지 조사하기 위해, 우리는 HIV1, HIV2, C형 간염, 뎅기-1, 홍역 바이러스, H. 필로리 박테리아, 인간 미토콘드리아 DNA의 유전자 배열 샘플에 이 방법을 적용했다. 또한 접근법의 가능한 한계, 특히 가능성을 추정하는 데 사용되는 모집단 모형의 잘못 지정에 대해 논의한다.
경험적 데이터: 경험적 데이터 세트는 이전 연구에서 추정된 바와 같이 다양한 수준의 재조합을 반영하기 위해 선택되었다(Maynard Smittheet al. 1993; Suerbaumet al. 1998; Awadalaet al. 1999; Worobeyet al. 1999; Ingmanet al). 2000; Worobey 2001). HIV 데이터 세트의 경우, 처음 두 위치와는 별도로 코딩 영역의 세 번째 위치 사이트를 분석하여, 다양성 수준이 다른 데이터를 사용하여 서로 다른 결과를 얻었는지 조사하였다. 또한 (Awadalaet al. 1999) 및 (Ingmanet al.)에 대한 증거를 제공하는 데 사용된 두 개의 인간 mtDNA 데이터 세트를 분석하였다. 2000) 재조합 모든 경우에 재조합을 위한 유전자 변환 모델이 교차합체 모델보다 더 적절하며, 우리는 바이러스 및 박테리아 데이터 세트의 경우 100bp, mtDNA 데이터 세트의 경우 500bp로 유전자 변환의 평균 트랙 길이를 고정했다. 미생물 및 바이러스 데이터 세트에서는 작은 트랙 길이에 대해 복합 가능성이 증가하지만(데이터는 표시되지 않음) 이러한 수치는 임의적이다. 유전자 변환 트랙 길이가 추정된 진핵생물의 몇 안 되는 사례 중 하나에서 데이터에 가장 적합한 것은 평균 트랙 길이가 352bp인 기하 분포였다(Hillikeret al. 1994).

표 3은 유전자 변환 유형 모델에서 이러한 분석의 결과와 모집단 재결합률 γ의 추정치를 보여준다. 식 5를 참조한다. 또한, 동일한 분석을 수행했지만, 경미한 알레르기가 주파수 <0.1>에 있었던 단일 뉴클레오티드 다형성(SNP)을 필터링하여 그 결과를 표 4에 제시하였다. HCV 및 뎅기 바이러스 데이터 세트의 경우, 표본 크기가 <10>이므로 여과된 분석의 결과는 표 2의 결과와 동일하다. Meunier와 Eyre-Walker(2001)는 |D ||와 거의 동일한 방식으로 동작하기 때문에 테스트 결과도 생략했다.
표 3에서 그리고 보다 눈에 띄게 표 4에서 우리는 HCV에서 inˆ=0.84 ~ HIV1에서 γˆ>100 범위의 거의 모든 데이터 집합과 재조합 수준에서 재조합을 위한 증거를 발견한다(γ = 100은 가능성이 추정된 한계인 만큼 컷오프로 선택되었다). HCV에서는 거리와의 r2의 상관관계만 유의한 음의 관계를 나타내지만, 6개의 시퀀스를 갖는 경우 우도 순열화 시험에서는 힘이 거의 없다. 홍역 데이터 세트의 경우, 모든 데이터를 사용할 때 r2만 유의하지만 필터링된 데이터에 대해 모든 검정은 유의하거나 약간 유의하다. 다른 데이터 집합은 훨씬 더 높은 수준의 재조합에 대한 증거를 보여준다. γ의 추정치는 H.필로리의 경우 40, 뎅기열의 경우 60이다. γˆ/θww 비율은 돌연변이에 대한 재결합 사건을 경험하는 뉴클레오티드의 상대적 가능성을 나타낸다. 재조합에 대한 강력한 지원이 있는 데이터 집합 내에서, 그 비율은 홍역의 경우 ~35에서 뎅기 및 H.필로리의 경우 ~1000까지 다양하며 잠재적으로 HIV1에서 훨씬 더 높다.
희귀 변종을 걸러내는 효과는 주목할 만하다. 희귀한 변형은 재조합에 대해 대체로 비정보적이므로(전부는 아니지만, McVean 2001), 따라서 그러한 변형이 포함되면 재조합의 신호를 모호하게 할 수 있으며, 특히 데이터에 희귀한 돌연변이가 과다한 경우 더욱 그러하다. 데이터에서 희귀 변형을 제거해도 경험적(표 3과 표 4의 비교 추정치)과 시뮬레이션 데이터의 모집단 재결합률 추정에는 거의 영향을 미치지 않는다. 예를 들어, 유한점모형에서 sites 추정치의 중위수는 모든 부위가 사용될 때(그리고 정확한 돌연변이 모델에 따라 분석했을 때) 9.8이었고, 분석은 경미한 알레르기가 0.1 이상인 부위로 제한되었을 때 10.2이었다. 시뮬레이션된 데이터에서 분석을 중간 주파수 변형으로 제한했을 때 우도 순열 시험의 검정력 증가는 발견되지 않았다. 그러나 시뮬레이션된 데이터 집합은 경험적 데이터와 달리 희귀한 변형을 초과하지 않는다.
Very high levels of recombination in HIV: HIV1 하위 유형 B와 HIV2 하위 유형 A 시퀀스의 재결합에 관한 결과가 특히 주목할 만하다. 비록 다른 하위 유형들 사이의 재조합이 때때로 관찰된다. (Kuikenet al. 2000), 하위 유형 내 재조합은 유전적 다양성의 유전학적 분석에서 크게 무시되었다(닐슨과 양 1998; 람보셋 al. 2001). 여기에 제시된 결과는 그러한 결론을 뒷받침한다. HIV1의 경우 SNP가 여과될 때만 HIV2와 HIV1에서 모두 재조합될 수 있는 증거를 찾을 수 있다. HIV1의 경우 γ의 추정치는 가능성이 추정된 범위를 벗어난다.
유전적 다양성의 수준은 HIV1과 HIV2에서 매우 높다(각각 0.144와 0.102의 1/2 코돈 위치에서 사이트당 ates의 추정치). 재발 돌연변이는 재조합에 의해 야기되는 것과 유사한 유전적 다양성의 패턴을 야기할 수 있기 때문에 재조합이 존재한다고 결론짓는 것은 조심스러울 수 있다. 그러나 훨씬 더 높은 수준의 다양성을 가진 HCV (θw=0.325) 와 유사한 수준의 시퀀스 다양성을 가진 홍역 ( measlesww=0.089) 에서 낮은 수준의 재조합을 추정하는 것은 높은 수준의 시퀀스 다양성이 반드시 인구 재조합률의 높은 추정으로 이어지는 것은 아니라는 것을 보여준다.

HIV1에서 그렇게 높은 수준의 재조합이 시사하는 바는 상당하다. 재조합의 부재를 가정해 만들어진 바이러스 역사상 사건의 나이와 시기에 대한 결론의 타당성에 의문을 제기할 뿐만 아니라(닐슨과 양 1998; 람보셋 al. 2001) 돌연변이(약물 저항성 등)가 다른 유전자에 얼마나 빨리 퍼질 수 있는지를 예측하는 데 실질적인 함의를 갖고 있다. 배경들 서로 다른 모집단 척도로 채취한 적절한 표본의 유전자 데이터의 분석은 재조합의 범위와 결과를 유추하는 데 필수적일 것이다.
Recombination in human mtDNA? 또 다른 중요한 문제는 인간 mtDNA에 재조합을 위한 증거가 있는지 여부다. Awadalla 외 연구진(1999)의 데이터 집합은 모든 데이터를 사용할 때 45개 시퀀스 중 35개 랜덤 하위 집합의 90% 이상에 대해서도 모든 데이터를 사용할 때 재조합을 위한 증거를 명확하게 보여준다. 직접적으로 대조적으로, 잉그만 외 연구소의 데이터. (2000) 사용된 시험에 관계 없이 재조합에 대한 증거를 표시하지 않는다. 주파수 필터가 적용될 때, 첫 번째 데이터 세트에서 재조합을 위한 증거를 보여주는 통계는 r2 하나뿐입니다(그리고 이것은 단일 분리 사이트의 제거에 민감하다). 이러한 결과는 거의 모든 테스트의 힘을 증가시키는 바이러스 및 박테리아 시퀀스에서의 결과와 직접적인 대조를 이룬다. 이 결과를 종합하면 인간 mtDNA의 재조합에 대한 증거가 부족하다는 것을 알 수 있다.
왜 저주파 변형이 재조합의 인상을 만들어야 하는가? 헤이(2000)는 시퀀싱 프로토콜이 상관관계가 있는 오류의 전파를 초래할 수 있다고 제안했다. 이러한 영향은 복수의 실험실에서 나온 결과의 조합에 의해 강화될 수 있으며(재발적인 오류는 강하게 상관될 것이기 때문이다), 그리고 이러한 이유로 잉그만 등이 수집하고 시퀀싱한 데이터는 다음과 같다. (2000년)이 바람직하다. 시퀀싱 오류가 저주파인 경향이 있다는 점을 감안할 때, 이는 4가지 테스트 중 3개가 모든 데이터를 분석해야 왜 유의한지 설명할 수 있지만, 고주파 변종만 사용해도 r2가 여전히 거리와 유의한 관계를 보이는 이유는 설명하지 않는다(우연한 범위를 초과). McVean(2001)은 국소 적응형 진화의 덩어리가 r2로 측정한 대로 상관관계가 있는 돌연변이와 물리적 거리와 연결부 불안정 사이의 관계를 유발할 수 있다고 제안했다. 적응형 진화가 불균형 연계 패턴에 어떻게 영향을 미치는지와 재조합의 측정과 검출은 중요한 문제다.

Misspecification of the population model: 모집단 재결합률에 대한 복합 우도 추정기의 특성을 다양한 시퀀스 진화 모델에 걸쳐 조사했지만, 여기에서 설명한 방법이 모집단 모델에서 얼마나 견고한지에 대해서는 지금까지 언급되지 않았다. 합체우도 추정은 무작위 짝짓기, 다른 모집단으로의 이동 또는 이동, 자연선택이 없는 일정한 크기의 모집단에서 무작위 표본을 추출했다고 가정한다. 실제로, 이러한 가정들 중 어느 것도 유효 모집단 크기 Ne에 영향을 미치는 것으로 표준 중립 모델(인구 크기 변동 등)에서 몇 가지 편차를 근사하게 추정할 수 있지만, 이 가정들 중 어느 것도 준수할 수 없다.
인구 증가, 강력한 지리적 구조화, 그리고 데이터베이스에서 유전자 서열의 비랜덤적 표현은 잠재적으로 결합 방법의 사용에 중요한 관심사다. 모집단 유전자 분석을 위해 특별히 시퀀스를 추출하는 것은 비랜덤 데이터베이스 표현 문제를 극복할 것이지만, 인구통계학적 모델의 불충분한 점은 더 문제가 있다. 인구 증가는 연계가 불안정해지는 경향을 보이는 반면, 인구 구조는 연계가 불안정해지는 경향을 보인다(예: 프리처드 및 프제워스키 2001). 따라서 인구 재결합률(및 재결합 탐지 능력)의 추정치는 모집단의 인구통계학적 이력에 민감할 것으로 예상할 수 있다.
여기서는 잘못 지정된 모집단 모델에서 CLE의 동작을 특성화하기 위한 철저한 시도를 하지 않지만, 분석된 데이터 세트가 알레르 주파수 스펙트럼 측면에서 중립 모델과의 편차에 대한 증거를 보이는지 여부를 물어볼 수 있다. 이것은 가장 간단하게 타지마 D 통계치를 이용하여 평가할 수 있는데, 이 통계치는 분리현장의 수와 평균 쌍별 차이에서 도출된 인구 돌연변이율의 추정치를 비교한다. 이 통계량의 음수 값은 희귀한 변종의 초과와 인구 증가 가능성을 나타내며, 양의 값은 인구 구조가 중요할 수 있음을 나타낸다.
표 3은 분석된 데이터 세트에 대한 타지마 D 통계량의 값을 포함하며, 재조합이 없다고 가정하여 추정된 유의 수준을 나타낸다. 이 통계량은 모든 데이터 집합에 대해 음수인 반면 홍역, HIV1 및 두 mtDNA 데이터 집합에 대해서는 유의하게만 해당된다. 그러나 통계량의 분산은 재조합에 의해 감소된다(그러므로 null 모형에 따른 신뢰 한계 감소). 따라서 다른 데이터 세트(특히 HIV2 데이터)도 표준 중립 모델에서 상당한 편차를 반영할 수 있다. 그러나 표준 중립 모델에서 벗어나는 증거를 보여주는 데이터 집합은 추정 재조합 비율의 완전한 다양성을 반영한다. 요컨대, 가정된 인구통계학적 모델로부터의 이탈이 인구 재결합률 추정에 어느 정도 영향을 미칠 수 있지만, 재결합 신호와 혼동될 가능성은 낮다.

댓글