ANOVA (ANalysis Of VAriance)
: 둘 이상 샘플들(그룹들)을 서로 비교하고자 할 때 집단 내의 분산, 총평균 그리고 각 집단의 평균의 차이에 의해 생긴 집단 간 분산의 비교를 통해 만들어진 F분포를 이용하여 가설검정을 하는 방법이다.
https://en.wikipedia.org/wiki/Analysis_of_variance
ANOVA는 Machine learning의 classification문제와 동일하다.
| Statistics | Machine Learning |
| 입력값 | Instance, X |
| 입력변수, 1개 One-way ANOVA, 2개 Two-way ANOVA, 2개 이상 MANOVA |
Feature, X.columns |
| 그룹 | Y |
두 샘플의 비교부터 알아보자.
T-test
두 샘플을 비교하는 가장 간단한 테스트는 T-test이다.
from scipy.stats import shapiro, ttest_ind
from statsmodels.graphics.gofplots import qqplot
shapiro(case) # check normality
# ShapiroResult(statistic=0.9600201845169067, pvalue=0.04715685546398163)
qqplot(case,line='s',label='Shapiro-Wilk\'s p-value\n: '+str(shapiro(case))
ttest_ind(case, ctrl) # it assumes that case and ctrl have identical variance
ttest_ind(case, ctrl, equal_var=False) # it assumes that case and ctrl have different variance
# Ttest_indResult(statistic=1.4065208204805022, pvalue=0.16201854576517558)T-test 이전에, 샘플들의 normality를 Shapiro-Wilk test를 통해 확인해 보자.
이 테스트는 샘플이 normal 분포를 따른다고 가정한다.
보통 P-value 기준을 0.05로 잡고 있고, P-value는 0.05 보다 낮은 값이 나왔으니 normal 분포가 아니라고 판단한다.

하지만 QQ plot에서 보면 normal 분포에 많이 벗어나지 않은 것으로 보인다. Normality test를 통해 얻은 p-value로 판단을 하기에는 고려해야할 요소들이 몇 가지 있다. 아래 링크 참고.
https://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless
T-test는 샘플들의 평균값을 비교하는 test로, 두 샘플이 같은 집단에서 나왔는지 아닌지 P-value로 판단한다.
위 T-test p-value는 0.16이고, 기준인 0.05로 해석해보면 '두 샘플은 같은 집단에서 나왔다'고 할 수 있다.
만약 비교할 샘플이 여러개이면 for문으로 해야하는데, 이를 위한 library가 있다.
비교 전에 여러 샘플들의 분포를 확인한다.

sns.boxplot(data=df,x='pheno', y='mean', order=order, palette="Set3", showfliers = False)
# boxprops={'facecolor':'None'}, whiskerprops={'linewidth':0}, showcaps=False, whiskerprops={'linewidth':0}
sns.swarmplot(data=df,x='pheno', y='mean', order=order, alpha=0.5, color='black')seaborn.boxplot(*, x=None, y=None, hue=None, data=None, order=None,
hue_order=None, orient=None, color=None, palette=None, saturation=0.75,
width=0.8, dodge=True, fliersize=5, linewidth=None, whis=1.5, ax=None,
**kwargs)
seaborn.swarmplot(x=None, y=None, hue=None, data=None,
order=None, hue_order=None, split=False, orient=None, color=None,
palette=None, size=5, edgecolor='gray', linewidth=0, ax=None,
**kwargs)
Box plot의 분포를 보면 전부 같은 집단으로 판단된다.
ANOVA를 통해 샘플들에서 다른 집단에서 나온것이 있는지 다음과 같인 확인한다. PR이 0.601437이라 샘플들은 같은 집단이다. 만약 0.05보다 낮은 PR이 나왔다면 사후검정으로 확인해 보자. ANOVA는 구체적으로 어떤 샘플들이 차이가 나는지 알 수 없다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols(formula='mean ~ pheno', data=df).fit()
print(model.summary())
print(anova_lm(model))
OLS Regression Results
==============================================================================
Dep. Variable: mean R-squared: 0.007
Model: OLS Adj. R-squared: -0.004
Method: Least Squares F-statistic: 0.6219
Date: Tue, 08 Jun 2021 Prob (F-statistic): 0.601
Time: 17:18:36 Log-Likelihood: -1551.7
No. Observations: 264 AIC: 3111.
Df Residuals: 260 BIC: 3126.
Df Model: 3
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 535.3965 11.236 47.651 0.000 513.272 557.521
pheno[T.B_ctrl] -18.6834 15.213 -1.228 0.221 -48.640 11.274
pheno[T.D_case] -9.3461 15.890 -0.588 0.557 -40.635 21.943
pheno[T.D_ctrl] -17.0775 15.213 -1.123 0.263 -47.035 12.880
==============================================================================
Omnibus: 87.602 Durbin-Watson: 1.949
Prob(Omnibus): 0.000 Jarque-Bera (JB): 444.969
Skew: 1.242 Prob(JB): 2.38e-97
Kurtosis: 8.855 Cond. No. 5.01
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
df sum_sq mean_sq F PR(>F)
pheno 3.0 1.413088e+04 4710.292024 0.621854 0.601437
Residual 260.0 1.969396e+06 7574.600785 NaN NaNANOVA에서 알 수 없었던 샘플 사이에 관계를 사후검정(post-hoc)을 통해 확인할 수 있다.
Bonferroni와 Tukey's HSD(honestly significant difference) test 로 확인한 결과 모두 p-value가 높게 나온다.
from statsmodels.sandbox.stats.multicomp import MultiComparison
from statsmodels.stats.multicomp import pairwise_tukeyhsd
comp = MultiComparison(df['mean'], df['pheno'])
result = comp.allpairtest(ttest_ind, method='bonf')
print(result[0])
Test Multiple Comparison ttest_ind
FWER=0.05 method=bonf
alphacSidak=0.01, alphacBonf=0.008
=============================================
group1 group2 stat pval pval_corr reject
---------------------------------------------
B_case B_ctrl 1.4038 0.1628 0.9766 False
B_case D_case 0.5794 0.5634 1.0 False
B_case D_ctrl 1.1351 0.2584 1.0 False
B_ctrl D_case -0.6071 0.5449 1.0 False
B_ctrl D_ctrl -0.1121 0.9109 1.0 False
D_case D_ctrl 0.4574 0.6482 1.0 False
---------------------------------------------
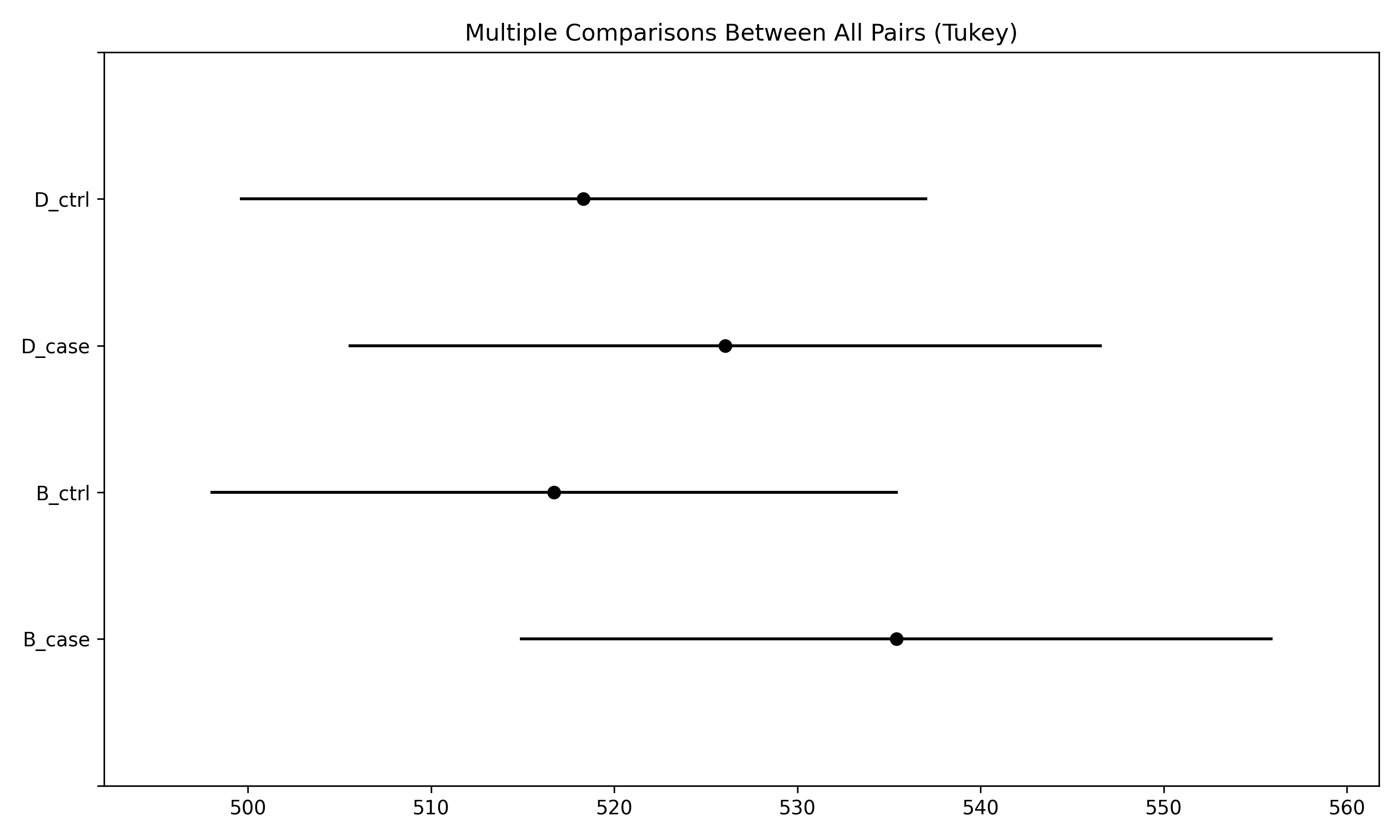
hsd = pairwise_tukeyhsd(df['mean'], df['pheno'], alpha=0.05)
hsd.plot_simultaneous()
print(hsd.summary())
Multiple Comparison of Means - Tukey HSD, FWER=0.05
=====================================================
group1 group2 meandiff p-adj lower upper reject
-----------------------------------------------------
B_case B_ctrl -18.6834 0.5966 -58.0226 20.6558 False
B_case D_case -9.3461 0.9 -50.4346 31.7423 False
B_case D_ctrl -17.0775 0.6557 -56.4167 22.2617 False
B_ctrl D_case 9.3372 0.9 -30.002 48.6765 False
B_ctrl D_ctrl 1.6059 0.9 -35.9026 39.1144 False
D_case D_ctrl -7.7314 0.9 -47.0706 31.6078 False
-----------------------------------------------------

Reference
- Comparison of Post Hoc Tests for Unequal Variance, Mital C. Shingala et. al. / International Journal of New Technologies in Science and Engineering Vol. 2, Issue 5,Nov 2015, ISSN 2349-0780
'Statistics' 카테고리의 다른 글
| Regression error (0) | 2021.07.04 |
|---|---|
| Multiple test correction (0) | 2021.06.10 |
| Fisher's exact test (0) | 2021.06.01 |
| SKAT-O (0) | 2021.01.06 |
| P-value (0) | 2020.11.30 |



댓글