Markov chain

Markov chain은 일정한 확률론적 규칙에 따라 한 상태에서 다른 상태로의 전이(transition)하는 수학적 시스템인 stochastic process이다. 이때 미래의 상태는 현재에 상태만 관련이 있고, 과거의 상태에 영향을 받지 않는 Markov property를 가지고 있다. Random walk도 markov property를 가지고 있다.

 

Stochastic and Markov process

Stochastic process는 indexed random variable의 collection을 말한다. Index는 time이 되는 경우가 많다.

[ Stochastic process but not Markov chain ]

Stochastic process이지만 Markov process가 아닌 경우의 예를 보자.
3가지 색깔을 가진 공이 여러 개 담긴 가방에서 random 하게 공을 꺼낼 때, 특정한 색깔의 공을 꺼낼 확율은 어떻게 될 것인가? 공을 꺼내는 것은 stochastic process지만, 나중에 공을 꺼낼때 특정 공을 꺼낼 확율이 달라지기 때문에 Markov process는 아니다.

 

[ Stochastic process and Markov chain ]

이번에는 Stochastic & Markov process인 경우를 보자.
세 가지 색깔의 공에서 random하게 하나를 선택하는 과정은 stochastic process이며, 이 공을 가방에 있는 공과 바꾸는 과정은 Markov process가 된다. 

 

정의와 용어, 수학적 표현 방식을 알아보자.

 

초기 확률 분포 (Initial probability distribution)이란, 처음 상태(state) i 에서의 확률이 π_i 이고 전체 S 상태가 있다고 할 때, 각 상태의 초기 확률의 집합을 말한다.

 

 

"i 상태에서 n번의 step을 거쳐 j 상태로 가는 확률"을 표현하면 다음과 같다.

 

Irreducible markov chain은 어느 상태에서 시작하던 n번의 step을 거쳐 모든 상태로 이동이 가능하다는 뜻이다.

 

 

Aperiodic하다는 말은 자신 상태로 다시 돌아오는 주기가 1이 있는 경우를 이야기 한다.

[ P_{2,2}>1 : Aperiodic markov chain ]

"유한한 상태"가 있고, "양수의 recurrent"하며 "aperiodic"이면, irreducible과 equivalent하다.

 

Random process의 stablility에 대한 정보를 주는 stationary distribution은 transition matrix P  를 가했을 때 자기 자신이 되는 π를 가리킨다.

 

[ Stationary distribution ]

 

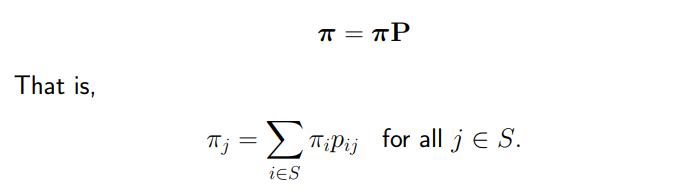
이때 π를 P에 대해서 invariant 하다고 한다.

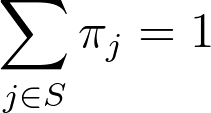
그리고 probability ditribution의 합이 1을 만족하면 unique solution을 가진다.

 

Limiting distribution은 어느 상태에서 시작하던, 무한번의 step을 거쳤을 때 j 상태가 되는 것을 이야기한다.

 

[ Property of Limiting distribution ]

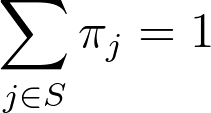
확률 값 π_j 을 알고 있으면, j 상태로 돌아오는 평균 시간을 구할 수 있다.

 

[ Mean return time ]

 

Some properties

 

 

Reference

- https://brilliant.org/wiki/markov-chains/

- https://en.wikipedia.org/wiki/Stochastic_process

- https://mast.queensu.ca/~stat455/lecturenotes/set3.pdf

- https://medium.com/@kim_hjun/markov-chain-stationary-distribution-5198941234f6

- https://www.probabilitycourse.com/chapter11/11_2_6_stationary_and_limiting_distributions.php

- blog.naver.com/jinis_stat/221687060317